Introduction
At the centre of the mastery approach to the teaching of mathematics is the belief that all pupils have the potential to succeed. They should have access to the same curriculum content and, rather than being extended with new learning, they should deepen their conceptual understanding by tackling challenging and varied problems. Similarly with calculation strategies, pupils must not simply rote learn procedures but demonstrate their understanding of these procedures through the use of concrete materials and pictorial representations.
This policy outlines the different calculation strategies that should be taught and used in Years 1-4, in line with the requirements of the 2014 Primary National Curriculum.
Background
The 2014 Primary National Curriculum for mathematics differs from its predecessor in many ways. Alongside the end of Key Stage year expectations, there are suggested goals for each year; there is also an emphasis on depth before breadth and a greater expectation of what pupils should achieve. In addition, there is a whole new assessment method, as the removal of levels gives schools greater freedom to develop and use their own systems.
One of the key differences is the level of detail included, indicating what pupils should be learning and when. This is suggested content for each year group, but schools have been given autonomy to introduce content earlier or later, with the expectation that by the end of each key stage the required content has been covered.
For example, in Year 2, it is suggested that pupils should be able to ‘add and subtract one-digit and two-digit numbers to 20, including zero’ and a few years later, in Year 5, they should be able to ‘add and subtract whole numbers with more than four digits, including using formal written methods (columnar addition and subtraction)’.
In many ways, these specific objectives make it easier for teachers to plan a coherent approach to the development of pupils’ calculation skills. However, the expectation of using formal methods is rightly coupled with the explicit requirement for pupils to use concrete materials and create pictorial representations – a key component of the mastery approach.
Purpose
The purpose of this policy is twofold. Firstly, it makes teachers aware of the strategies that pupils are formally taught within each year group that will support them to perform mental and written calculations. Secondly, it supports teachers in identifying appropriate pictorial representations and concrete materials to help develop understanding.
The policy only details the strategies; teachers must plan opportunities for pupils to apply these; for example, when solving problems, or where opportunities emerge elsewhere in the curriculum.
How to use the policy
For ease of reference, the strategies and examples contained in this policy are cross-referenced with objectives from the 2014 Maths Programme of Study. For each of the four rules of number, different strategies are laid out, together with examples of what concrete materials can be used and how, along with suggested pictorial representations. Please note that the concrete and representation examples are not exhaustive, and teachers and pupils may well come up with alternatives. Where necessary, additional guidance is given to support in teaching the given strategies.
Please note that the principle of the concrete-pictorial-abstract (CPA) approach is that for pupils to have a true understanding of a mathematical concept, they need to master all three phases. Reinforcement is achieved by going back and forth between these representations. For example, if a child has moved on from the concrete to the pictorial, it does not mean that the concrete cannot be used alongside the pictorial. Or if a child is working in the abstract, ‘proving’ something or ‘working out’ could involve use of the concrete or pictorial. In short, these are not always ‘exclusive’ representations.
Mathematical language
The 2014 National Curriculum is explicit in articulating the importance of pupils using the correct mathematical language as a central part of their learning. Indeed, in certain year groups, the non-statutory guidance highlights the requirement for pupils to extend their language around certain concepts.
2014 Maths Programme of Study
It is therefore essential that teaching using the strategies outlined in this policy is accompanied by the use of appropriate mathematical vocabulary. New vocabulary should be introduced in a suitable context (for example, with relevant real objects, apparatus, pictures or diagrams) and explained carefully. High expectations of the mathematical language used are essential, with teachers only accepting what is correct.
| Tick | Cross |
|---|---|
| ones | units |
| is equal to | equals |
| zero | oh (the letter O) |
Exemplification
You will see that throughout this document, calculations are presented in a variety of ways,. It is important for pupils’ mathematical understanding to experience and work with calculations and missing numbers in different positions relative to the = symbol. Examples used in classwork and independent work should reflect this.
Estimation
Pupils are expected to use their developing number sense from Year 1 to make predictions about the answers to their calculations. As their range of mental strategies increases, these predictions and, later, estimates should become increasingly sophisticated and accurate. All teaching of calculation should emphasise the importance of making and using these estimates to check, first, the sense and, later, the accuracy of their calculations.
end faq
Progression in calculations Year 1
National Curriculum objectives linked to addition and subtraction
These objectives are explicitly covered through the strategies outlined in this document:
- Add and subtract one-digit and two-digit numbers to 100, including zero (N.B. Year 1 N.C. objective is to do this with numbers to 20).
- Add and subtract numbers using concrete objects, pictorial representations, and mentally, including: a two-digit number and ones, a two-digit number and tens, 2 two-digit numbers; add 3 one-digit numbers (Year 2).
- Represent and use number bonds and related subtraction facts within 20.
- Given a number, identify 1 more and 1 less.
- Show that addition of two numbers can be done in any order (commutative) but subtraction of one number from another cannot (Year 2).
- Recognise the inverse relationship between addition and subtraction and use this to solve missing number problems (Year 2).
The following objectives should be planned for lessons where new strategies are being introduced and developed:
- Read, write and interpret mathematical statements involving addition (+), subtraction (−) and equal (=) signs.
- Solve one-step problems that involve addition and subtraction, using concrete objects and pictorial representations, and missing number problems, such as 7 = □ − 9.
- Solve problems with addition and subtraction:
- Using concrete objects and pictorial representations, including those involving numbers, quantities and measures
- Applying their increasing knowledge of mental methods
Addition
| Strategy & guidance | CPA |
|---|---|
|
Joining two groups and then recounting all objects using one-to-one correspondence |
 |
|
Counting on As a strategy, this should be limited to adding small quantities only (1, 2 or 3) with pupils understanding that counting on from the greater is more efficient. Pupils should be encouraged to rely on number bonds knowledge as time goes on, rather than using counting on as their main strategy. |
 |
|
Part-part-whole Teach both addition and subtraction alongside each other, as pupils will use this model to identify the inverse link between them. Pupils could place ten on top of the whole as well as writing it down. The parts could also be written in alongside the concrete representation. This model begins to develop the understanding of the commutativity of addition, as pupils become aware that the parts will make the whole in any order. |
 |
|
Regrouping ten ones to make ten This is an essential skill that will support column addition later on. |
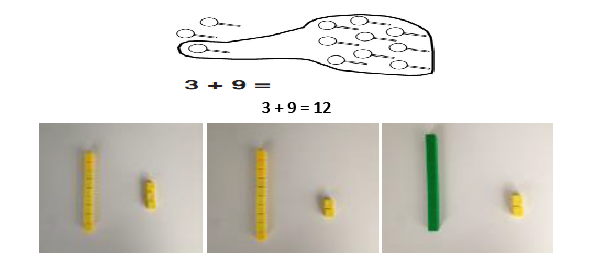 |
|
‘Make ten’ strategy Pupils should be encouraged to start at the bigger number and use the smaller number to make ten. The colours of the beads on the bead string make it clear how many more need to be added to make ten. Also, the empty spaces on the ten frame make it clear how many more are needed to make ten. |
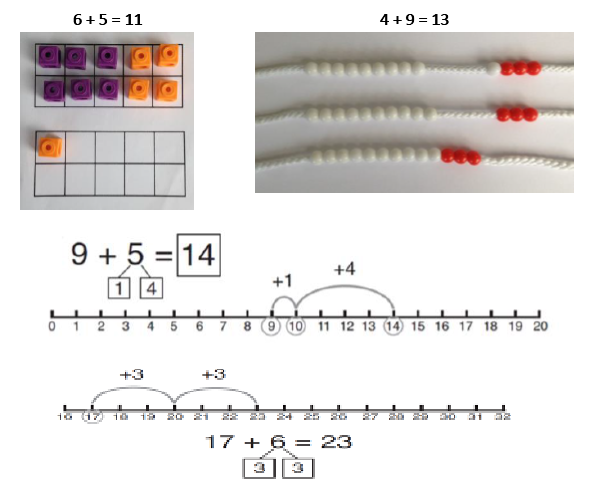 |
|
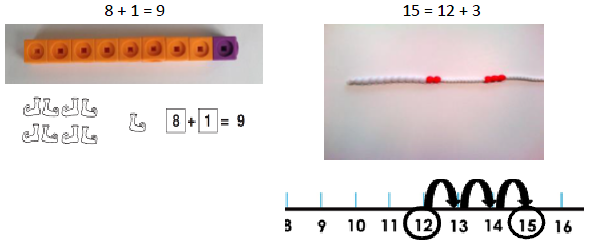
Adding 1, 2, 3 more Here the emphasis should be on the language rather than the strategy. As pupils are using the beadstring, ensure that they are explaining using language such as; ‘1 more than 5 is equal to 6.’ ‘2 more than 5 is 7.’ ‘8 is 3 more than 5.’ |
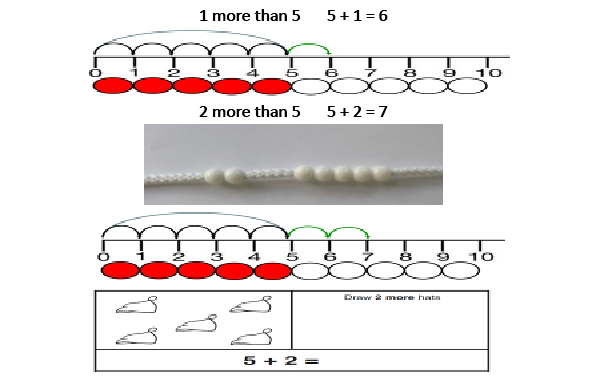 |
|
Adding three single digit numbers (make ten first) Pupils may need to try different combinations before they find the two numbers that make 10. The first bead string shows 4, 7 and 6. The colours of the bead string show that it makes more than ten. The second bead string shows 4, 6 and then 7. The final bead string shows how they have now been put together to find the total. |
 |
|
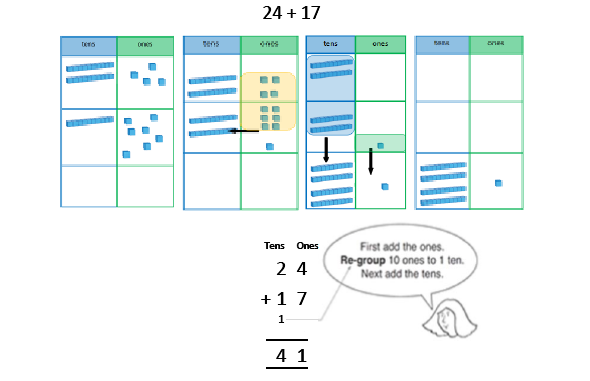
Partitioning to add (no regrouping) Place value grids and Dienes blocks should be used as shown in the diagram before moving onto the pictorial representations. Dienes blocks should always be available, as the main focus in Year 1 is the concept of place value rather than mastering the procedure. When not regrouping, partitioning is a mental strategy and does not need formal recording in columns. This representation prepares them for using column addition with formal recording. See additional guidance on unit pages for extra guidance on this strategy. |
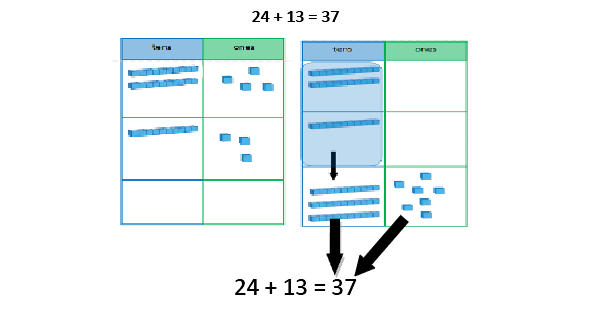 |
|
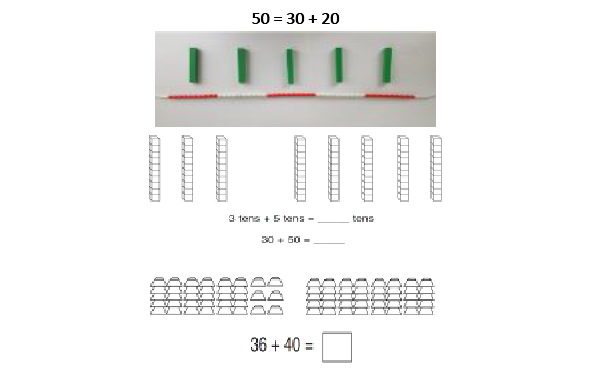
Adding multiples of ten Using the vocabulary of 1 ten, 2 tens, 3 tens etc. alongside 10, 20, 30 is important, as pupils need to understand that it is a ten and not a one that is being added. It also emphasises the link to known number facts. E.g. ‘2 + 3 is equal to 5. So 2 tens + 3 tens is equal to 5 tens. |
 |
|
Partitioning to add (no regrouping) Place value grids and Dienes blocks should be used as shown in the diagram before moving onto the pictorial representations. Dienes blocks should always be available, as the main focus in Year 1 is the concept of place value rather than mastering the procedure. When not regrouping, partitioning is a mental strategy and does not need formal recording in columns. This representation prepares them for using column addition with formal recording. See additional guidance on unit pages for extra guidance on this strategy. |
 |
Subtraction
| Strategy & guidance | CPA |
|---|---|
|
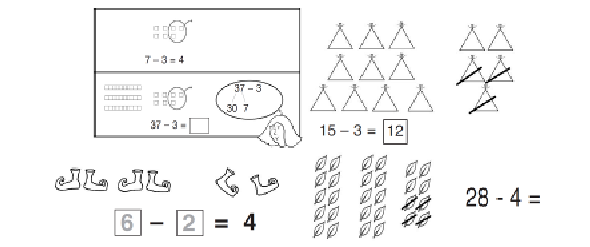
Taking away from the ones When this is first introduced, the concrete representation should be based upon the diagram. Real objects should be placed on top of the images as one-to-one correspondence so that pupils can take them away, progressing to representing the group of ten with a tens rod and ones with ones cubes. |
 |
|
Counting back Subtracting 1, 2, or 3 by counting back Pupils should be encouraged to rely on number bonds knowledge as time goes on, rather than using counting back as their main strategy. |
 |
|
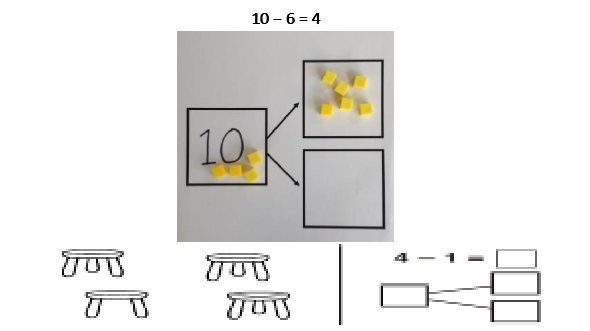
Part-part-whole Teach both addition and subtraction alongside each other, as the pupils will use this model to identify the link between them. Pupils start with ten cubes placed on the whole. They then remove what is being taken away from the whole and place it on one of the parts. The remaining cubes are the other part and also the answer. These can be moved into the second part space. |
 |
|
‘Make ten’ strategy single digit number from a 2-digit number Pupils identify how many need to be taken away to make ten first. Then they take away the rest to reach the answer. |
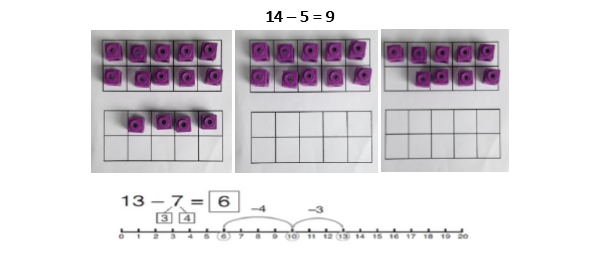 |
|
Regroup a ten into 10 ones After the initial introduction, the Dienes blocks should be placed on a place value chart to support place value understanding. This will support pupils when they later use the column method. |
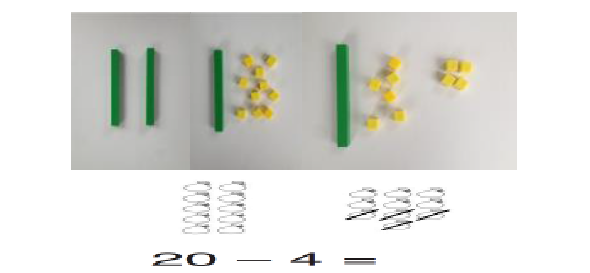 |
|
Taking away from the tens Pupils should identify that they can also take away from the tens and get the same answer. This reinforces their knowledge of number bonds to 10 and develops their application of number bonds for mental strategies. |
 |
|
Partitioning to subtract without regrouping Dienes blocks on a place value chart (developing into using images on the chart) should be used, as when adding 2-digit numbers, reinforcing the main concept of place value for Year 1. When not regrouping, partitioning is a mental strategy and does not need formal recording in columns. This representation prepares them for using column subtraction with formal recording. See additional guidance on unit pages to support with this strategy. |
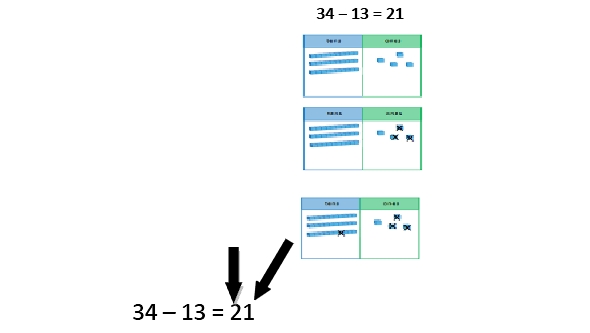 |
|
Subtracting multiples of ten Using the vocabulary of 1 ten, 2 tens, 3 tens etc. alongside 10, 20, 30 is important as pupils need to understand that it is a ten not a one that is being taken away. |
 |
|
Column method with regrouping This example shows how pupils should work practically when being introduced to this method. There is no formal recording in columns in Year 1 but this practical work will prepare pupils for formal methods in Year 2. See additional guidance on unit pages to support with this method. |
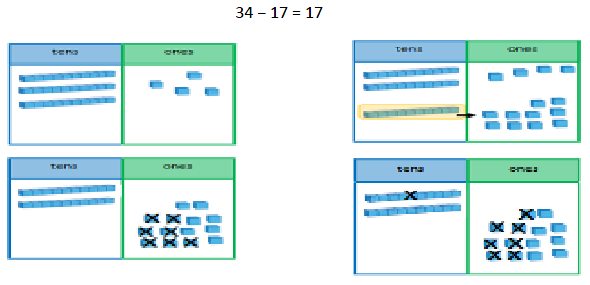 |
end faq
National Curriculum objectives linked to multiplication and division
These objectives are explicitly covered through the strategies outlined in this document:
Solve one-step problems involving multiplication and division, by calculating the answer using concrete objects, pictorial representations and arrays with the support of the teacher.
Multiplication
| Strategy & guidance | CPA |
|---|---|
|
Skip counting in multiples of 2, 5, 10 from zero The representation for the amount of groups supports pupils’ understanding of the written equation. So two groups of 2 are 2, 4. Or five groups of 2 are 2, 4, 6, 8, 10. Count the groups as pupils are skip counting. Number lines can be used in the same way as the bead string. Pupils can use their fingers as they are skip counting. |
 |
|
Making equal groups and counting the total How this would be represented as an equation will vary. This could be 2 × 4 or 4 × 2. The importance should be placed on the vocabulary used alongside the equation. So this picture could represent 2 groups of 4 or 4 twice. |
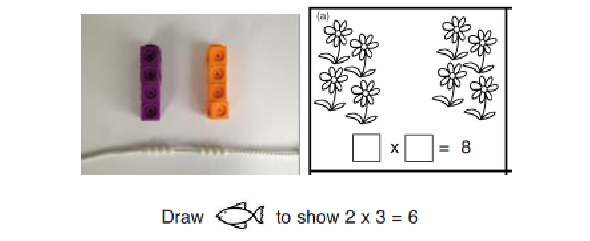 |
|
Solve multiplications using repeated addition |
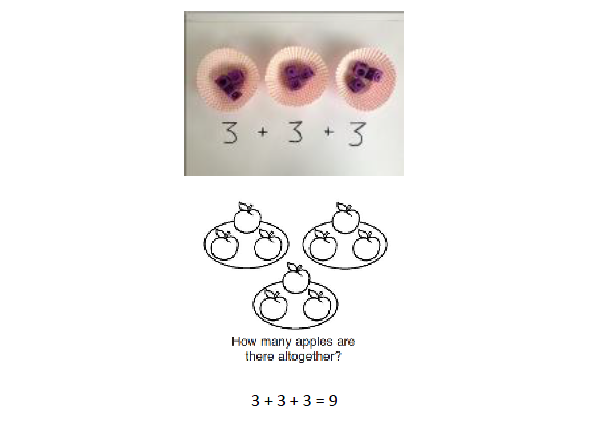 |
Division
| Strategy & guidance | CPA |
|---|---|
|
Sharing objects into groups Pupils should become familiar with division equations through working practically. The division symbol is not formally taught at this stage. |
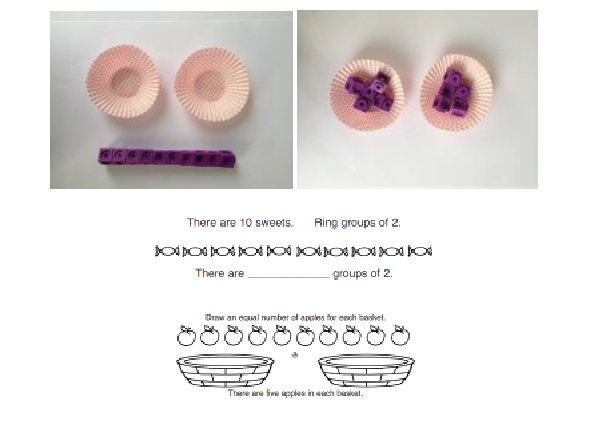 |
end faq
end faq
Progression in calculations Year 2
National Curriculum objectives linked to addition and subtraction
These objectives are explicitly covered through the strategies outlined in this document:
- Add and subtract numbers using concrete objects, pictorial representations, and mentally, including: a two-digit number and ones; a two-digit number and tens; 2 two-digit numbers; adding three one-digit numbers.
- Add and subtract numbers mentally, including: a three-digit number and ones; a three-digit number and tens; a three-digit number and hundreds (Year 3).
- Recall and use addition and subtraction facts to 20 fluently, and derive and use related facts up to 100.
- Find 10 or 100 more or less than a given number (Year 3).
- Show that addition of two numbers can be done in any order (commutative) but subtraction of one number from another cannot.
- Recognise and use the inverse relationship between addition and subtraction and use this to check calculations and solve missing number problems.***
- Add and subtract numbers with up to three digits, using formal written methods of columnar addition and subtraction (Year 3).
The following objectives should be planned for lessons where new strategies are being introduced and developed:
- Solve problems with addition and subtraction: using concrete objects and pictorial representations, including those involving numbers, quantities and measures; apply increasing knowledge of mental and written methods.
- Solve problems, including missing number problems, using number facts, place value and more complex addition and subtraction. (Year 3)
Addition
| Strategy & guidance | CPA |
|---|---|
|
Partitioning one number, then adding tens and ones Pupils can choose themselves which of the numbers they wish to partition. Pupils will begin to see when this method is more efficient than adding tens and taking away the extra ones, as shown. |
 |
|
Rounding one number, then adding the tens and taking away extra ones Pupils will develop a sense of efficiency with this method, beginning to see when rounding and adjusting is more efficient than adding tens and then ones. |
 |
|
Counting on in tens and hundreds |
 |
|
Partitioning to add without regrouping As in Year 1, this is a mental strategy rather than a formal written method. Pupils use the Dienes blocks (and later, images) to represent 3-digit numbers but do not record a formal written method if there is no regrouping. |
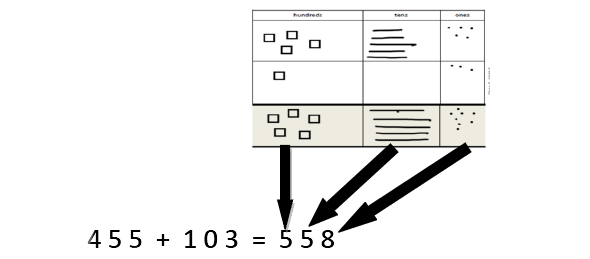 |
|
Column method with regrouping Dienes blocks should be used alongside the pictorial representations; they can be placed on the place value grid before pupils make pictorial representations. As in Year 1, the focus for the column method is to develop a strong understanding of place value. See additional guidance on unit pages for extra guidance on this strategy. |
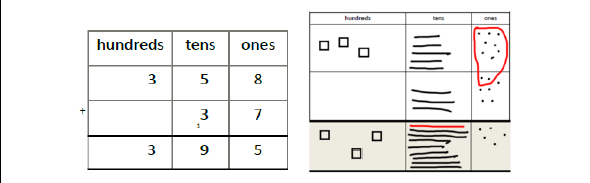 |
|
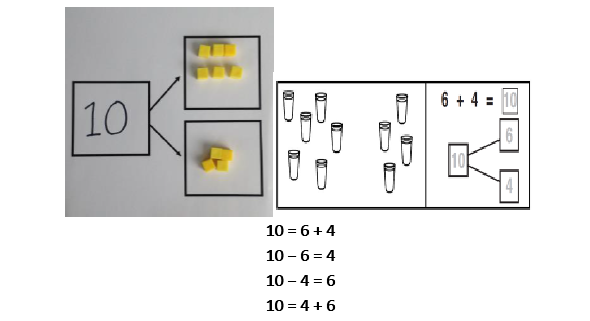
Part-part-whole Pupils explore the different ways of making 20. They can do this with all numbers using the same representations. This model develops knowledge of the inverse relationship between addition and subtraction and is used to find the answer to missing number problems. |
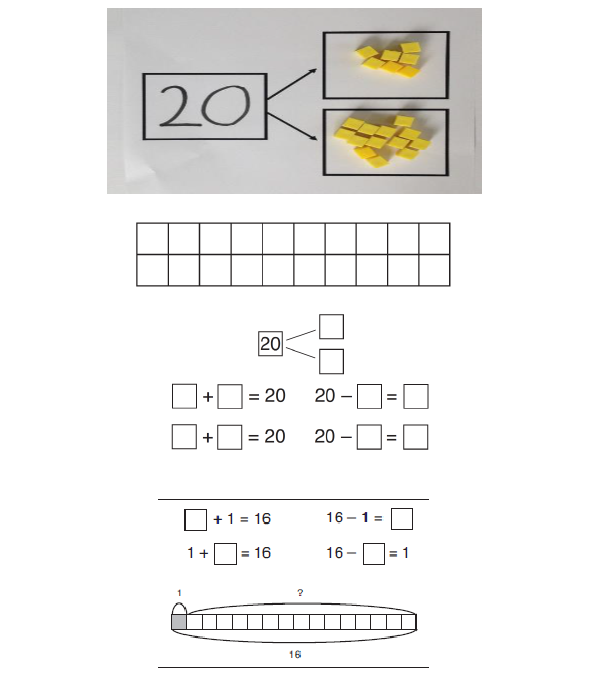 |
|
Make ten strategy How pupils choose to apply this strategy is up to them; however, the focus should always be on efficiency. |
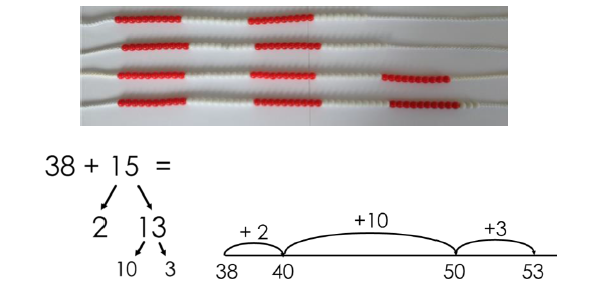 |
|
Using known facts Dienes blocks should be used alongside pictorial and abstract representations when introducing this strategy. |
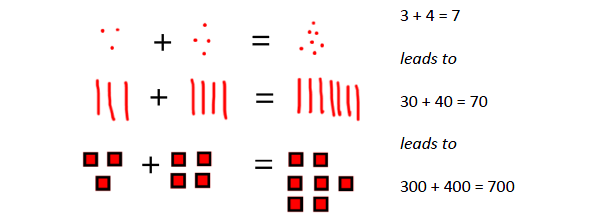 |
Subtraction
| Strategy & guidance | CPA |
|---|---|
|
Subtracting tens and ones Pupils must be taught to partition the second number for this strategy. Pupils will begin to see when this method is more efficient than subtracting tens and adding the extra ones, as shown. |
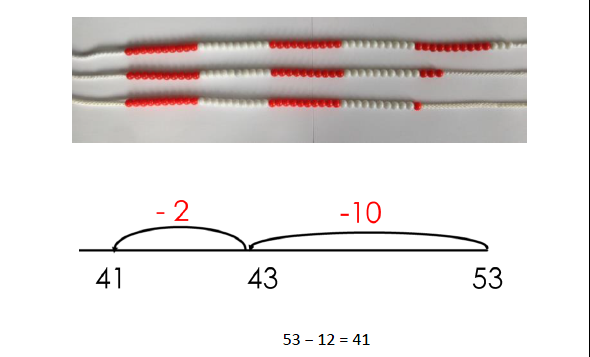 |
|
Subtracting tens and adding extra ones Pupils must be taught to round the number that is being subtracted. Pupils will develop a sense of efficiency with this method, beginning to identify when this method is more efficient than subtracting tens and then ones. |
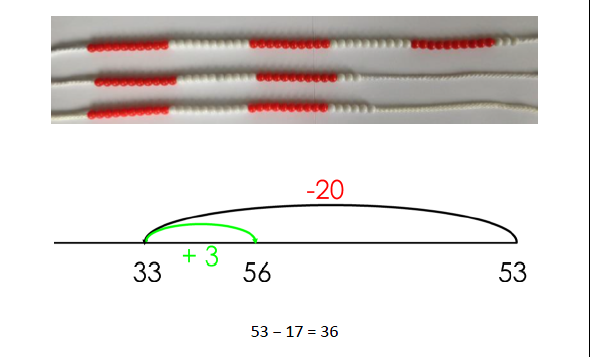 |
|
Counting back in multiples of ten and one hundred |
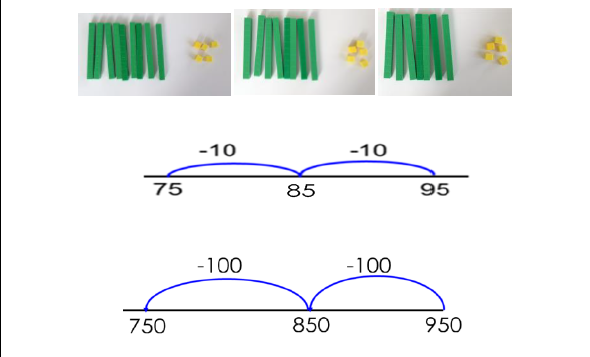 |
|
Partitioning to subtract without regrouping As in Year 1, the focus is to develop a strong understanding of place value and pupils should always be using concrete manipulatives alongside the pictorial. Formal recording in columns is unnecessary for this mental strategy. It prepares them to subtract with 3-digits when regrouping is required. Please also see additional guidance on unit pages for extra guidance on this strategy. |
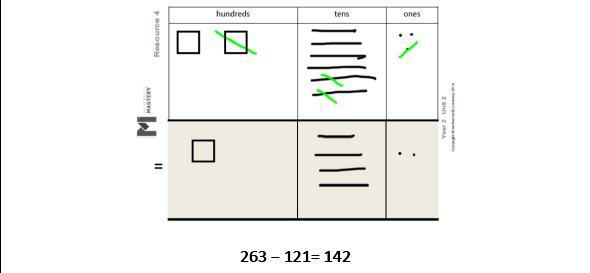 |
|
Column method with regrouping As in Year 1, the focus for the column method is to develop a strong understanding of place value and pupils should always be using concrete manipulatives alongside the pictorial. Pupils are introduced to calculations that require two instances of regrouping (initially from tens to one and then from hundreds to tens). E.g. 232 – 157 and are given plenty of practice using concrete manipulatives and images alongside their formal written methods, ensuring that important steps are not missed in the recording. Caution should be exercised on introducing calculations requiring ‘regrouping to regroup’ (e.g. 204 – 137) ensuring ample teacher modelling using concrete manipulatives and images. |
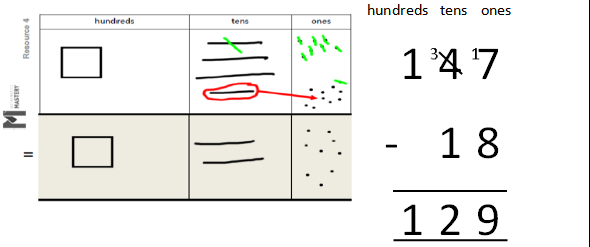 |
|
Bridging through ten How pupils choose to apply this strategy is up to them. The focus should always be on efficiency. |
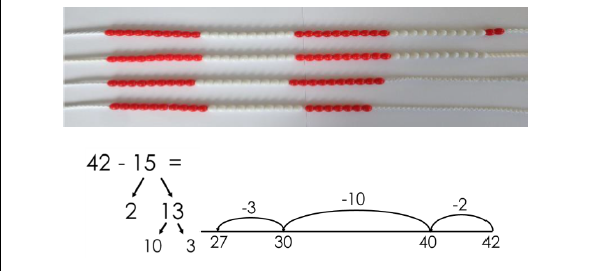 |
|
Using known number facts Dienes blocks should be used alongside pictorial and abstract representations when introducing this strategy. |
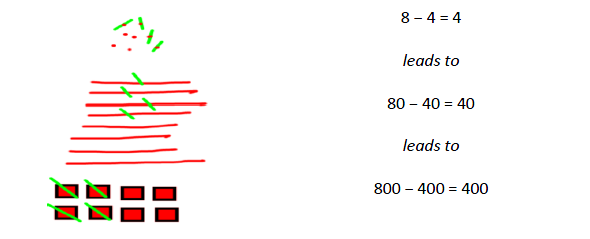 |
end faq
National Curriculum objectives linked to multiplication and division
These objectives are explicitly covered through the strategies outlined in this document:
- Recall and use multiplication and division facts for the 2, 5 and 10 multiplication tables, including recognising odd and even numbers.
- Recall and use multiplication and division facts for the 3 and 4 multiplication tables (Year 3).
- Show that multiplication of two numbers can be done in any order (commutative) but division of one number by another cannot.
The following objectives should be planned for lessons where new strategies are being introduced and developed:
- Calculate mathematical statements for multiplication and division within the multiplication tables and write them using the multiplication (×), division (÷) and equal (=) signs.
- Solve problems involving multiplication and division, using materials, arrays, repeated addition, mental methods and multiplication and division facts, including problems in context.
Multiplication
| Strategy & guidance | CPA |
|---|---|
|
Skip counting in multiples of 2, 3, 4, 5, 10 from 0 Pupils can use their fingers as they are skip counting, to develop an understanding of ‘groups of’. Dotted paper is used to create a visual representation for the different multiplication facts. Each multiplication table has its own template, which is provided during taught units.
|
 |
|
Multiplication as repeated addition Pupils will apply skip counting to help find the totals of these repeated additions. |
 |
|
Arrays to represent multiplication equations Concrete manipulatives and images of familiar objects begin to be organised into arrays and, later, are shown alongside dot arrays. It is important to discuss with pupils how arrays can be useful. Pupils begin to understand multiplication in a more abstract fashion, applying their skip counting skills to identify the multiples of the 2x, 5x and 10x tables. The relationship between multiplication and division also begins to be demonstrated. |
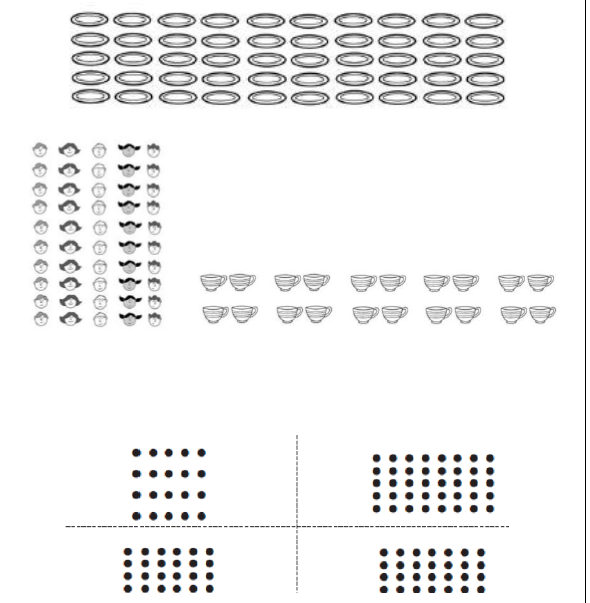 |
|
Multiplication is commutative Pupils should understand that an array and, later, bar models can represent different equations and that, as multiplication is commutative, the order of the multiplication does not affect the answer. |
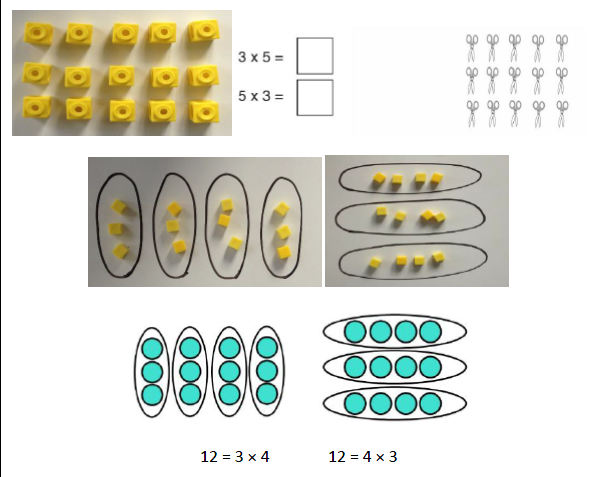 |
|
Bar modelling to represent the parts, the whole and the number of parts in multiplication word problems Cuisenaire rods can be used to create bar models that represent multiplications. |
 |
|
Use of part-partwhole model to establish the inverse relationship between multiplication and division This link should be made explicit from early on, using the language of the part-part-whole model, so that pupils develop an early understanding of the relationship between multiplication and division. Bar models (with Cuisenaire rods) should be used to identify the whole, the size of the parts and the number of parts. |
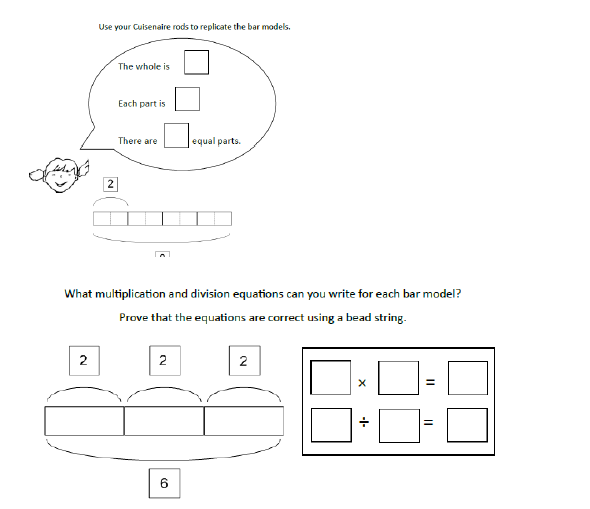 |
|
Doubling to derive new multiplication facts Pupils learn that known facts from easier times tables can be used to derive facts from related times tables using doubling as a strategy. At this stage they double the 2x table facts to derive the 4x table facts. |
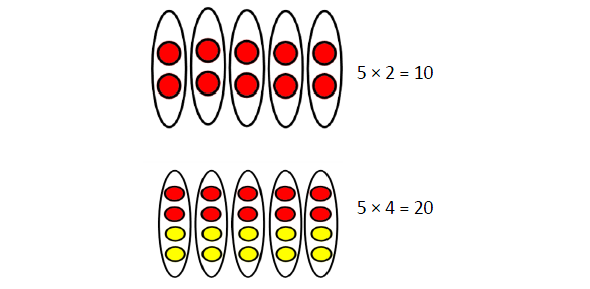 |
Division
| Strategy & guidance | CPA |
|---|---|
|
Division as sharing Here, division is shown as sharing. If we have ten pairs of scissors and we share them between two pots, there will be 5 pairs of scissors in each pot. |
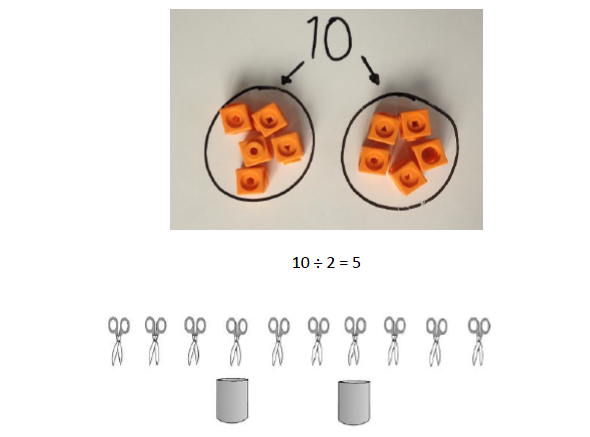 |
|
Division as grouping Here, division is shown as grouping. If we have ten forks and we put them into groups of two, there are 5 groups. |
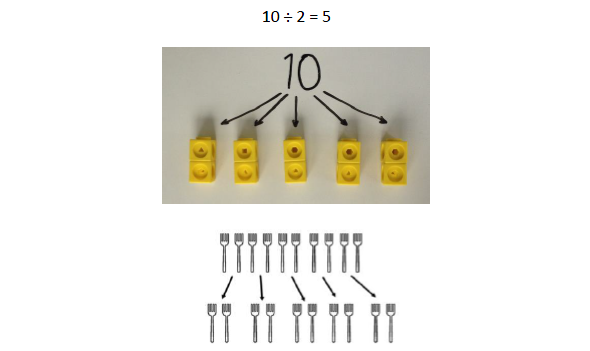 |
|
Use of part-part-whole model to represent division equations and to emphasise the relationship between division and multiplication Pupils use arrays of concrete manipulatives and images of familiar objects to find division equations. They begin to use dot arrays to develop a more abstract concept of division. |
 |
end faq
end faq
Progression in calculations Year 3
National Curriculum objectives linked to addition and subtraction
These objectives are explicitly covered through the strategies outlined in this document:
- add and subtract numbers mentally, including:
- a three-digit number and ones
- a three-digit number and tens
- a three-digit number and hundreds
- add and subtract numbers with up to four digits, using formal written methods of columnar addition and subtraction (four digits is Year 4)
- find 10 or 100 more or less than a given number
- find 1 000 more or less than a given number (Year 4)
- estimate the answer to a calculation and use inverse operations to check answers***
The following objectives should be planned for lessons where new strategies are being introduced and developed:
- solve problems, including missing number problems, using number facts, place value, and more complex addition and subtraction
Addition & Subtraction
| Strategy & guidance | CPA | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Add and subtract numbers mentally, including:
Pupils learn that this is an appropriate strategy when they are able to use known number-facts and other mental strategies to complete mental calculations with accuracy. To begin with, some pupils will prefer to use this strategy only when there is no need to regroup, using number facts within 10 and derivations. More confident pupils might choose from a range of mental strategies that avoid regrouping, including (but not exhaustively): known number facts within 20, derived number facts, make ten, compensation (see Year 2 guidance for exemplification of these – the use of concrete manipulatives other than Dienes blocks is important in reinforcing the use of these other strategies). It is important that pupils are given plenty of (scaffolded) practice at choosing their own strategies to complete calculations efficiently and accurately. Explicit links need to be made between familiar number facts and the calculations that they can be useful for and pupils need to be encouraged to aim for efficiency. |
See Year 2 – using the same strategies and, where required, manipulatives with numbers appropriate to the unit pupils are working within (3-digit or 4-digit numbers) e.g.
|
||||||||||||||||||||
|
Written column method for calculations that require regrouping with up to 4-digit numbers Dienes blocks should be used alongside the pictorial representations during direct teaching and can be used by pupils both for support and challenge. Place value counters can also be introduced at this stage. This work revises and reinforces ideas from Key Stage 1, including the focus on place value – see Year 2 exemplification. It is vital that pupils are made aware that this is one possible strategy and that they must decide which is the most efficient to make an accurate calculation. Direct teaching of the columnar method should require at least one element of regrouping, so that pupils are clear about when it is most useful to use it. Asking them ‘Can you think of a more efficient method?’ will challenge them to apply their number sense / number facts to use efficient mental methods where possible. As in Year 2, pupils should be given plenty of practice with calculations that require multiple separate instances of regrouping. In Year 3 they become more familiar with calculations that require ‘regrouping to regroup’. Understanding must be secured through the considered use of manipulatives and images, combined with careful use of language. Pupils should be challenged as to whether this is the most efficient method, considering whether mental methods (such as counting on, using known number facts, compensation etc.) may be likelier to produce an accurate solution. Pupils requiring support might develop their confidence in the written method using numbers that require no regrouping. See additional guidance on unit pages for extra guidance on this strategy. |
See Year 2 – Using the same strategies and concrete manipulatives but working with numbers that are appropriate to the unit pupils are working on. e.g.
|
||||||||||||||||||||
|
Find 10, 100 and 1000 more or less than a given number
|
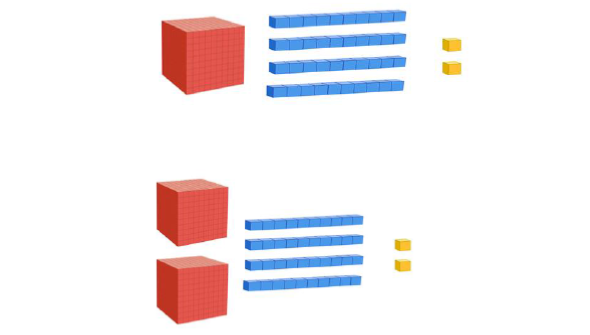 |
||||||||||||||||||||
end faq
National Curriculum objectives linked to multiplication and division
These objectives are explicitly covered through the strategies outlined in this document:
- count from 0 in multiples of 4, 8, 50 and 100
- recall and use multiplication and division facts for the 3, 4, 6, and 8 multiplication tables
- write and calculate mathematical statements for multiplication and division using the multiplication tables that they know, including for two-digit numbers times one-digit numbers, using mental methods
- solve problems, including missing number problems, involving multiplication and division, including positive integer scaling problems and correspondence problems in which n objects are connected to m objects
Multiplication
| Strategy & guidance | CPA |
|---|---|
|
Doubling to derive new multiplication facts Pupils continue to make use of the idea that facts from easier times tables can be used to derive facts from related times tables using doubling as a strategy. This builds on the doubling strategy from Year 2. |
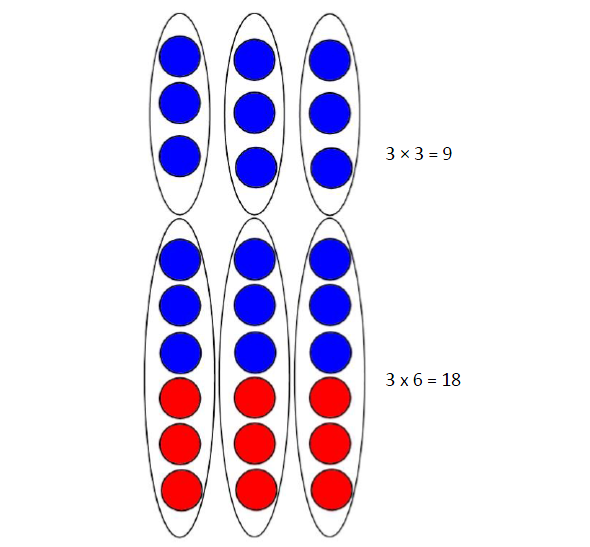 |
|
Skip counting in multiples of 2, 3, 4, 5, 6, 8 and 10 Rehearsal of previously learnt tables as well as new content for Year 3 should be incorporated into transition activities and practised regularly. |
 |
|
Use of part-part-whole model with arrays and bar models to establish commutativity and inverse relationship between multiplication and division In these contexts pupils are able to identify all the equations in a fact family. |
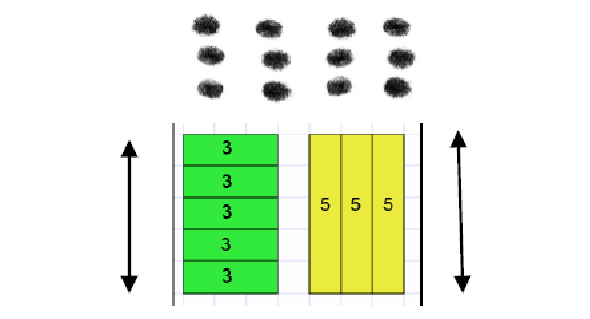 |
|
Ten times bigger Pupils’s work on this must be firmly based on concrete representations – the language of ten times bigger must be well modelled and understood to prevent the numerical misconception of ‘adding 0’. |
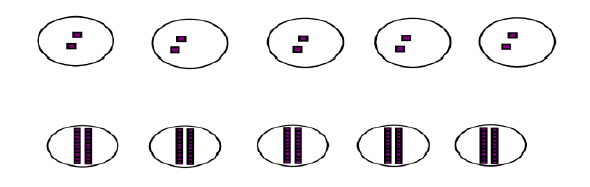 |
|
Multiplying by 10, 100 and 1000 Building on the ten times bigger work, pupils use appropriate Dienes blocks and place value counters to multiply 2, 3, 4, 5 and 10 by 10, 100 and 1000. |
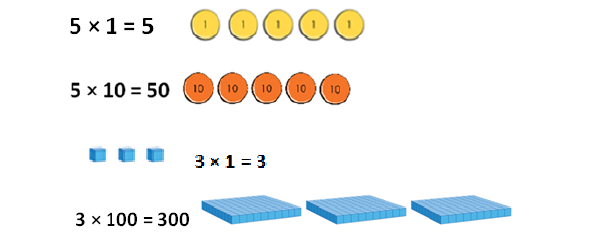 |
|
Using known facts for multiplying by multiples of 10, 100 and 1000 Pupils’ growing understanding of place value, allows them to make use of known facts to derive multiplications using powers of 10. It is important to use tables with which they are already familiar (i.e. not 7 or 9 tables in Year 3) |
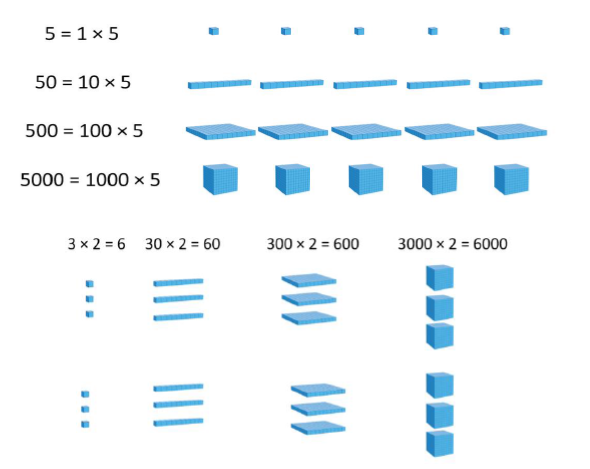 |
|
Multiplication of 2-digit numbers with partitioning (no regrouping) Children should always consider whether partitioning is the best strategy – if it is possible to use strategies such as doubling (some may use doubling twice for ×4), they need to choose the most efficient strategy. Children may wish to make jottings, including a full grid as exemplified here – but grid method is not a formal method and its only purpose is to record mental calculations. This supports the development of the necessary mental calculating skills but does not hinder the introduction of formal written methods in Year 4. Concrete manipulatives are essential to develop understanding. |
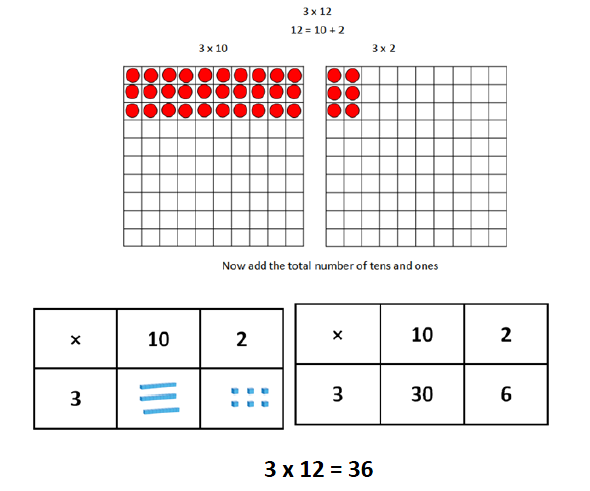 |
|
Multiplication of 2-digit numbers with partitioning (regrouping) Using concrete manipulatives and later moving to using images that represent them, supports pupils’ early understanding, leading towards formal written methods in Year 4. Once again, this is a mental strategy, which they may choose to support with informal jottings, including a full grid, as exemplified here. |
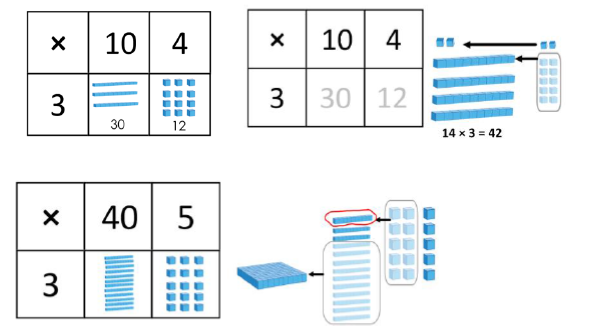 |
Division
| Strategy & guidance | CPA |
|---|---|
|
Dividing multiples of 10, 100 and 1000 by 10, 100 and 1000 Pupils use the strategy of sharing into equal groups of tens, hundreds or thousands to reinforce their understanding of place value and the concept of division as sharing into equal groups. They master this skill with calculations where no partitioning is required, to prepare them for the next step |
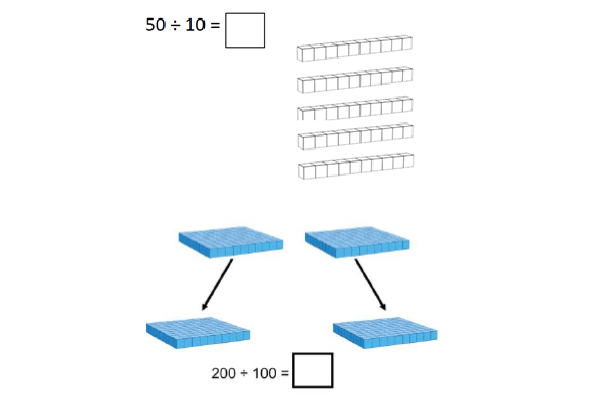 |
|
Division by partitioning and sharing into equal groups with no regrouping required Pupils apply the skills of sharing into equal groups, dividing 2-digit numbers by 3, 4 and 5. They should be encouraged not to use this strategy to divide by 2 (using halving instead). |
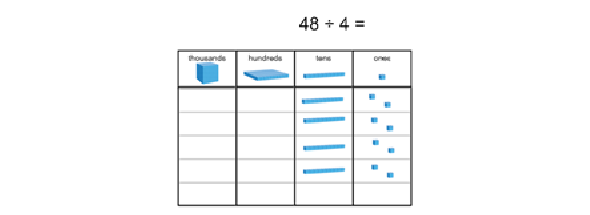 |
end faq
end faq
Progression in calculations Year 4
National Curriculum objectives linked to addition and subtraction
These objectives are explicitly covered through the strategies outlined in this document:
- add and subtract numbers with up to four digits, using the formal written methods of columnar addition and subtraction where appropriate
- find 1 000 more or less than a given number (Year 4)
- estimate answers and use inverse operations to check answers to a calculation***
N.B. There is no explicit reference to mental calculation strategies in the programmes of study for Year 4 in the national curriculum. However, with an overall aim for fluency, appropriate mental strategies should always be considered before resorting to formal written procedures, with the emphasis on pupils making their own choices from and increasingly sophisticated range of strategies.
The following objectives should be planned for lessons where new strategies are being introduced and developed:
- solve addition and subtraction two-step problems in contexts, deciding which operations and methods to use and why
- solve simple measure and money problems involving fractions and decimals to two decimal places
Addition & Subtraction
| Strategy & guidance | CPA |
|---|---|
|
Add and subtract multiples of 10, 100 and 1000 mentally By Year 4 pupils are confident in their place value knowledge and are calculating mentally both with calculations that do not require regrouping and with those that do. Initially they count on and back in steps of ten, one hundred and one thousand. These should be practised regularly, ensuring that boundaries where more than one digit changes are included. In Year 4, pupils extend this knowledge to mentally adding and subtracting multiples of 10, 100 and 1000. Counting in different multiples of 10, 100 and 1000 should be incorporated into transition activities and practised regularly. |
See Y3 guidance on mental addition & subtraction, remembering that use of concrete manipulatives and images in both teaching and reasoning activities will help to secure understanding and develop mastery. |
|
Written column methods for addition and subtraction |
Age appropriate calculations in Year 4 will begin to include some addition and subtraction of decimals (in context). Exemplification of this will be added in the coming months. |
end faq
National Curriculum objectives linked to multiplication and division
These objectives are explicitly covered through the strategies outlined in this document:
- count from 0 in multiples of 6, 7, 9, 25 and 1000
- recall and use multiplication and division facts for multiplication tables up to 12 × 12
- write and calculate mathematical statements for multiplication and division using the multiplication tables that they know, including for two-digit numbers times one-digit numbers, using mental and progressing to formal written methods
- recognise and use factor pairs and commutativity in mental calculations
- use place value, known and derived facts to multiply and divide mentally, including: multiplying by 0 and 1; dividing by 1; multiplying together three numbers
- multiply two-digit and three-digit numbers by a one-digit number using formal written layout
- find the effect of dividing a one- or two-digit number by 10 and 100, identifying the value of the digits in the answer as ones, tenths and hundredths
The following objectives should be planned for lessons where new strategies are being introduced and developed:
- solve problems involving multiplying and adding, including using the distributive law to multiply two digit numbers by one digit, integer scaling problems and harder correspondence problems such as n objects are connected to m objects
Multiplication
| Strategy & guidance | CPA |
|---|---|
|
Using known facts and place value for mental multiplication involving multiples of 10 and 100 Pupils use their growing knowledge of multiplication facts, place value and derived facts to multiply mentally. Emphasis is place on understanding the relationship (10 times or 100 times greater) between a known number fact and one to be derived, allowing far larger ‘fact families’ to be derived from a single known number fact. Knowledge of commutativity is further extended and applied to find a range of related facts. |
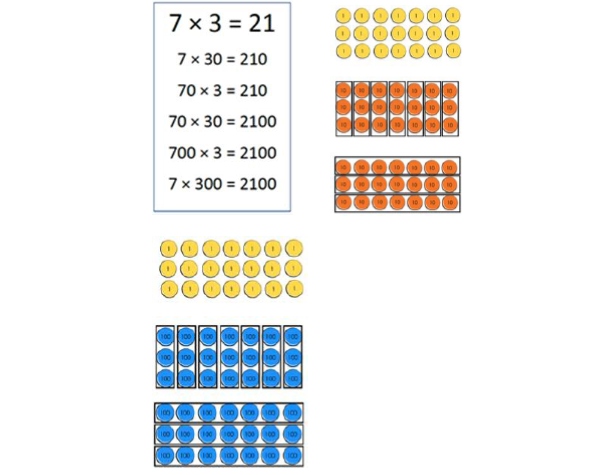 |
|
Mental multiplication of any 2-digit number by a 1-digit number, using distributive law Pupils build on mental multiplication strategies and develop an explicit understanding of distributive law, which allows them to explore new strategies to make more efficient calculations. As well as partitioning into tens and ones (a familiar strategy), they begin to explore compensating strategies and factorisation to find the most efficient solution to a calculation. |
|
|
Mental multiplication of 3 1-digit numbers, using the associative law Pupils first learn that multiplication can be performed in any order, before applying this to choose the most efficient order to complete calculations, based on their increasingly sophisticated number facts and place value knowledge. |
|
|
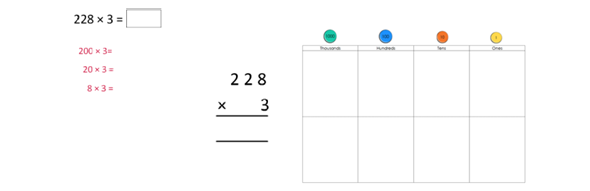
Short multiplication of 3-digit number by 1-digit number To begin with pupils are presented with calculations that require no regrouping or only regrouping from the ones to the tens. Their conceptual understanding is supported by the concomitant use of place value counters, both during teacher demonstrations and during their own practice. With practice pupils will be able to regroup in any column, including from the hundreds to the thousands, including being able to multiply numbers containing zero and regrouping through multiple columns in a single calculation. |
Exemplification of this process is best understood through viewing the Year 4 Unit 3 ‘Training Task’ (which can be found slightly further down the page from the Unit Tutorial here in the online toolkit)
|
Division
| Strategy & guidance | CPA |
|---|---|
|
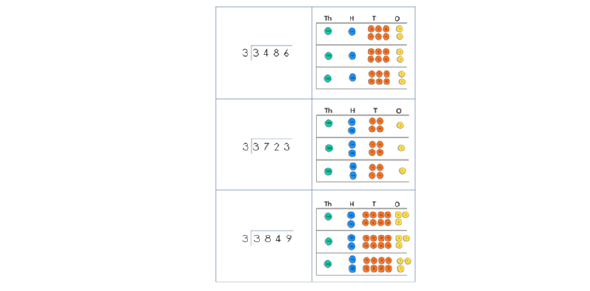
Short division of 4-digit numbers by 1-digit numbers Pupils start with dividing 4-digit numbers by 2, 3 and 4, where no regrouping is required. Place value counters are used simultaneously in a place value chart, to develop conceptual understanding. They progress to calculations that require regrouping in the hundreds or tens columns. Pupils build on their conceptual knowledge of division to become confident with dividing numbers where the tens digit is smaller than the divisor, extending this to any digit being smaller than the divisor. |
Exemplification of this process is best understood through viewing the Year 4 Unit 3 ‘Training Task’ (which can be found slightly further down the page from the Unit Tutorial here in the online toolkit)
|
|
Division of a one- or two-digit number by 10 and 100, identifying the value of the digits in the answer as ones, tenths and hundredths |
Exemplification of this will be added in the coming months. |
end faq
end faq
end faq
September 2015